TODO sobre las Funciones (matemáticas): teoría, ejemplos,...

¡Bienvenid@ a funciones.xyz!

En esta página web encontrarás la explicación de todos los temas relacionados con las funciones matemáticas. Cada artículo está explicado con ejemplos y, además, incluyen ejercicios resueltos paso a paso para practicar. ¡Además cualquier duda que tengas puedes preguntarla en los comentarios del artículo! Y tranquil@, ¡todo el contenido es gratuito! 😉😘

Características de las funciones

Dominio y recorrido de funciones
Tipos de funciones
Función inversa
Composición de funciones
Simetría de una función
Función acotada
Periodicidad de una función
Puntos de corte de una función
Operaciones con funciones
Transformaciones de funciones

Límites de funciones

Límite de una función
Límites al infinito
Limites laterales
Propiedades de los límites
Indeterminaciones
Continuidad de una función
Tipos de discontinuidades
Asíntotas de una función

Derivadas

Dominio y recorrido de funciones
Tabla de derivadas
Regla de la cadena
Ecuación de la recta tangente
Máximos y mínimos
Puntos de inflexión
Problemas de optimización
Representación de cualquier función

Integrales

Tabla de integrales
Integrales indefinidas
Integrales definidas
Propiedades de las integrales
Métodos de integración
Teorema fundamental del cálculo
Área bajo una función

Índice

¿Qué son las funciones?

En matemáticas, las funciones son expresiones algebraicas que relacionan dos magnitudes diferentes. Es decir, las funciones matemáticas relacionan cada elemento de una magnitud con un único elemento de otra magnitud.

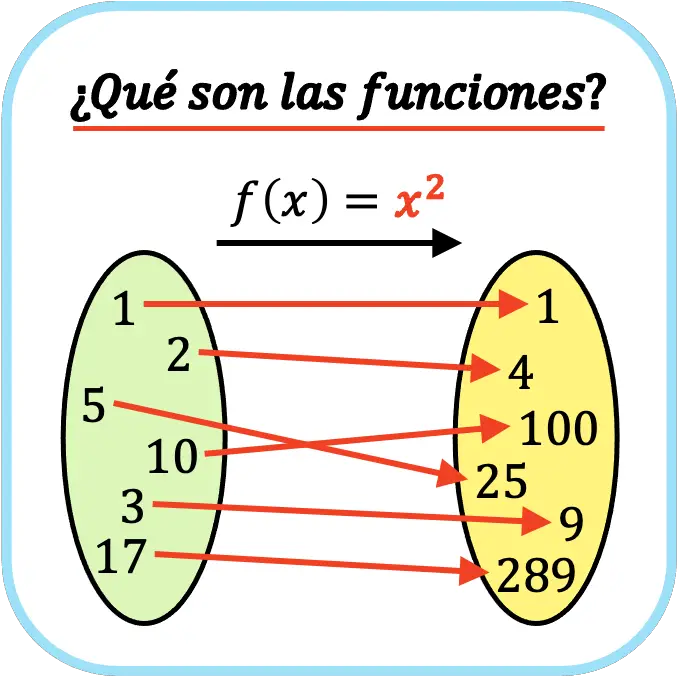
Por ejemplo, se puede relacionar matemáticamente la velocidad de una persona con el tiempo que tardará en recorrer un tramo utilizando una función. De manera que sabiendo la velocidad de la persona, se puede calcular el tiempo que tardará mediante una función matemática.

Las funciones se expresan mediante la letra y o con el símbolo f(x) indistintamente:

$y = f(x)$

Donde x es la variable independiente e y es la variable independiente.

Ejemplos de funciones

Vista la definición matemática de función, ahora vamos a ver varios ejemplos de funciones para acabar de entender su significado.

Función de primer grado:

$f(x)=3x+1$

Función de segundo grado:

$f(x)=x^2-5x+7$

Función con fracciones:

$f(x)=\cfrac{x^2+1}{x}-\cfrac{5x^3}{4}$

Aunque más abajo veremos cómo se representa gráficamente una función, a continuación puedes ver otro ejemplo de una función en este caso representada en un gráfico:

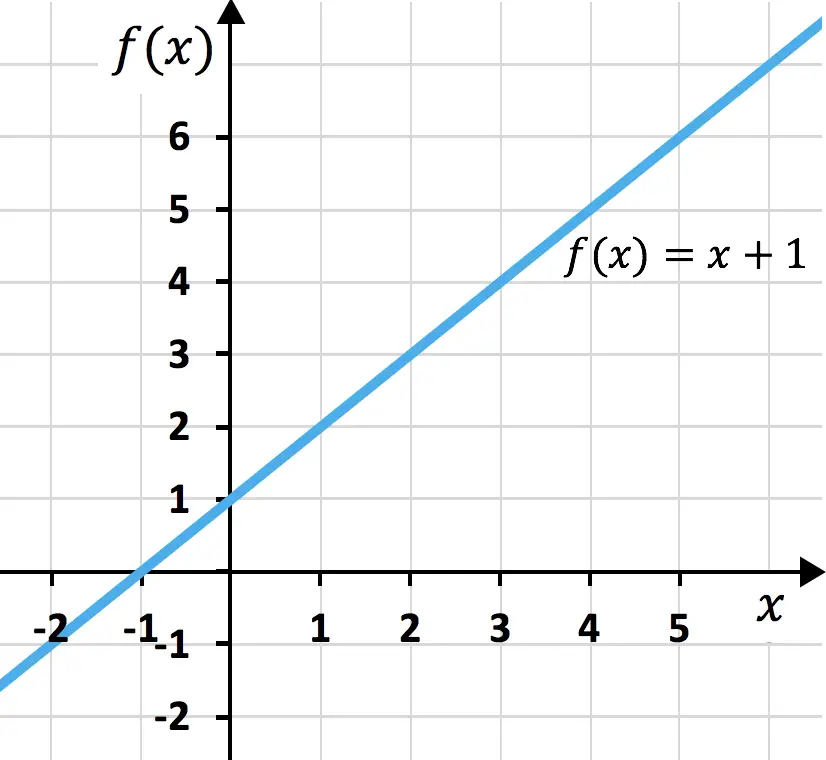
representacion grafica de una funcion matematica

Como ves en la gráfica, cuando $x$ es $2$ , $f(x)$ es $3$ . Esto se escribe de la siguiente manera:

$f(2)=3$

También lo podríamos haber calculado numéricamente sustituyendo la x por su valor correspondiente en la expresión de la función:

$f(x)=x+1$

$f(2)=2+1=3$

Ten en cuenta que para que una expresión se considere una función matemática solo puede existir un único valor de la función para cada valor de x.

Representación gráfica de funciones

En este apartado veremos cómo representar una función en una gráfica. Para ello, resolveremos un ejercicio paso a paso e iremos explicando el método mientras resolvemos el ejercicio.

Representa en una gráfica la siguiente función:

$f(x)=2x-1$

Lo primero que debemos hacer es crear una tabla de valores. Para ello vamos otorgando los valores que queramos a $x$ para obtener valores de $f(x)$ :

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

Cuan más puntos calculemos, más precisa será la representación gráfica de la función.

Una vez hemos creado la tabla de valores, representamos los puntos en el gráfico:

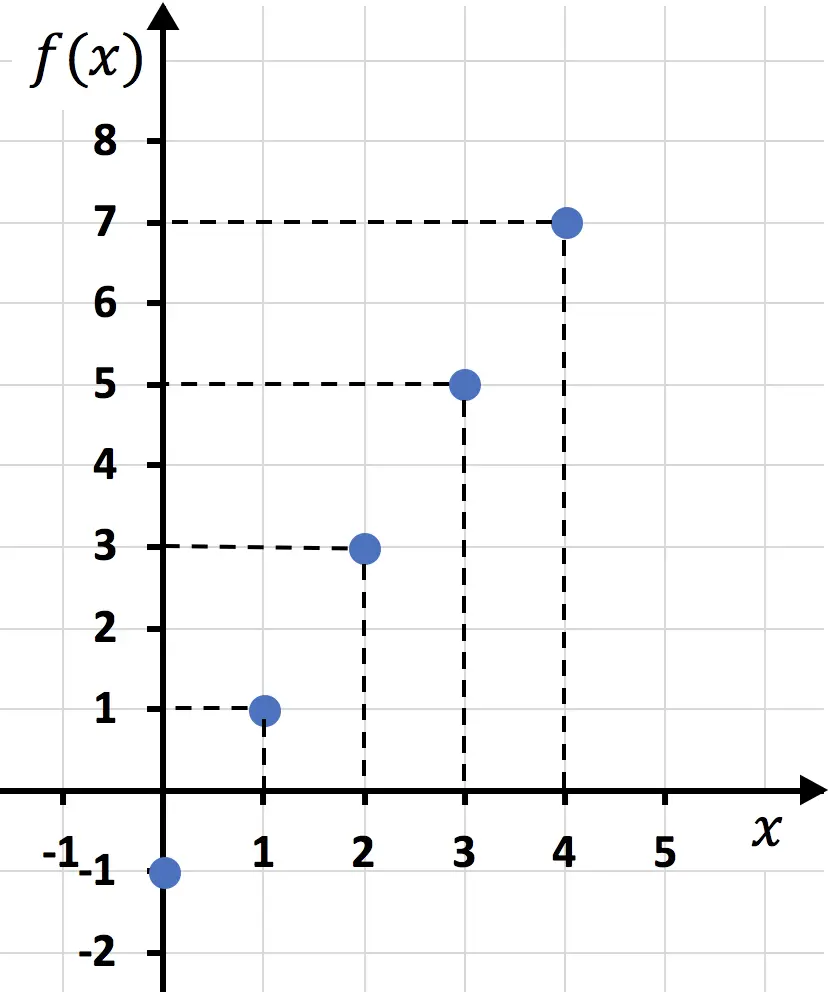
como representar graficamente una funcion

Y, finalmente, unimos los puntos y trazamos una línea entre ellos:

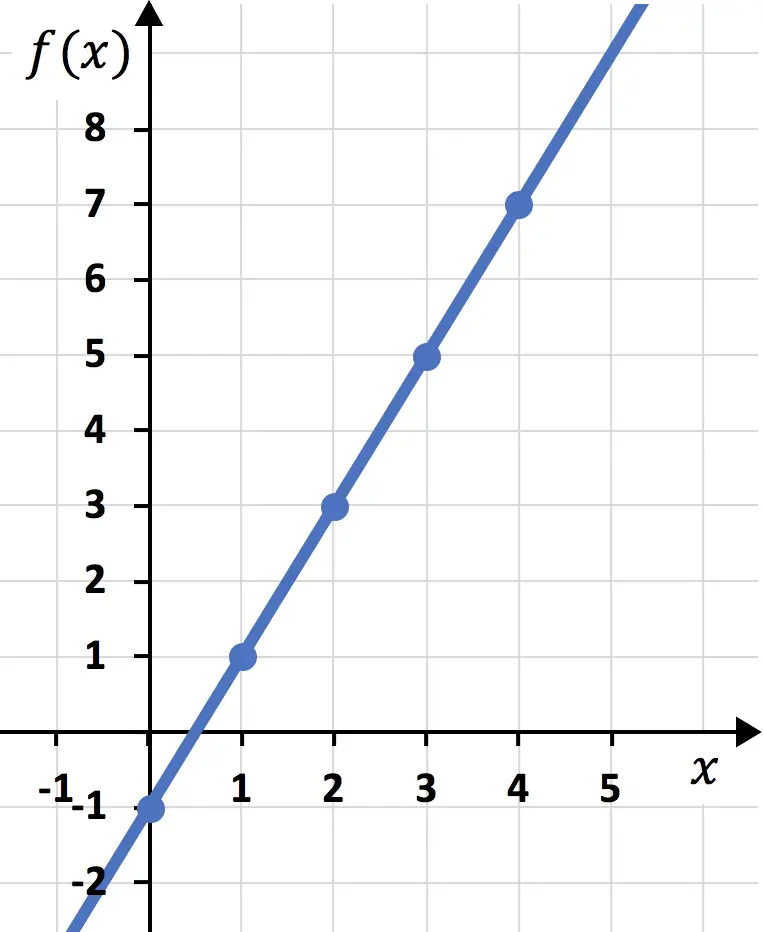
Dominio y recorrido de una función

Otros dos conceptos muy importantes de las funciones son su dominio y su recorrido, cuyas definiciones son las siguientes:

El dominio de una función real son todos los valores de x en los que existe la función. El dominio de una función se representa con la expresión Dom f.

El recorrido de una función, o imagen de una función, son todos los valores de f(x) donde existe la función. El recorrido de una función se representa con la expresión: Im f.

En matemáticas, el dominio de una función también se puede decir dominio de definición o campo de existencia. Por otro lado, se conoce el recorrido de una función como rango de una función.

Para entender mejor este concepto de las funciones, analizaremos el dominio y el recorrido de la siguiente función:

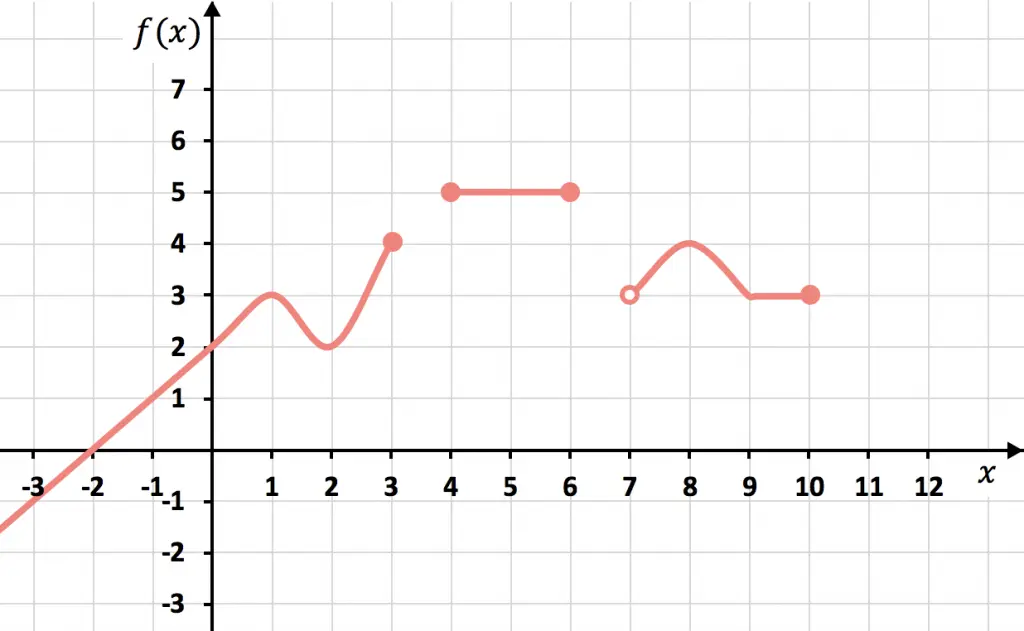
calcular el dominio y el recorrido de una funcion a partir del grafico

Primero examinaremos el dominio de la función, por lo que nos tenemos que fijar en el eje horizontal. La función viene desde $x=-\infty$ (porque no vemos donde empieza y no tiene ningún punto fijo al prinicipio) y existe hasta $x=3$ . Además, entre $x=4$ y $x=6$ también existe la función. Y la función existe incluso desde $x=7$ (no incluido) hasta $x=10$ , donde se acaba. Así que el dominio de la función es:

$\text{Dom } f= (-\infty,3]\cup [4,6] \cup (7,10]$

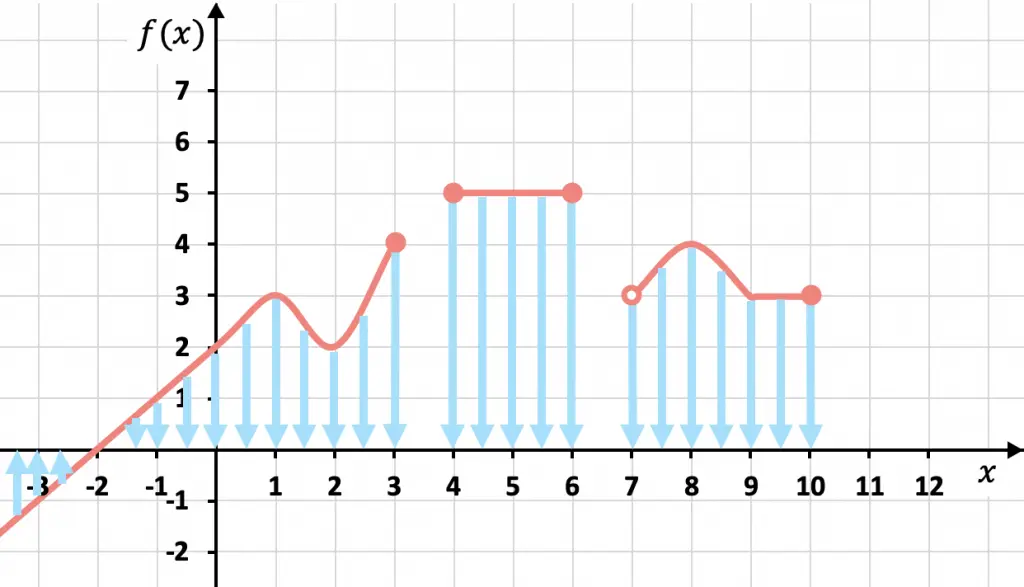
ejemplo de como calcular el dominio de una funcion graficamente

Si te fijas, desde $x=3$ hasta $x=4$ no existe la función, por lo tanto, este tramo no pertenece al domino de la función. Y lo mismo sucede con el tramo entre $x=6$ y $x=7$ , donde la función tampoco existe. Por eso no hemos incluido estos tramos en el dominio.

Recuerda que si tenemos un punto abierto, como en $x=7$ , hay que poner un paréntesis $"("$ o $")"$ , que indica que ese punto no está incluido, es decir que la función no existe en ese punto. En cambio, si tenemos un punto cerrado, como en $x=3$ , hay que poner un corchete $"["$ o $"]"$ , que indica que ese punto sí que está incluido. Asimismo, el infinito siempre va acompañado de un paréntesis ya sea positivo o negativo.

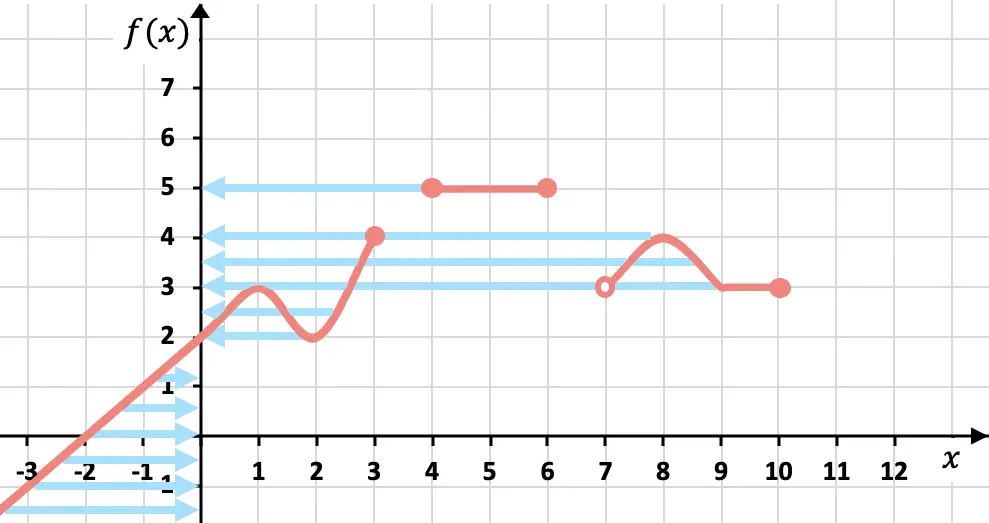
Ahora vamos analizar el recorrido de la función, y para ello nos tenemos que fijar en el eje vertical. La función viene desde $f(x)=-\infty$ y existe hasta $f(x)=4$ , por lo tanto, este tramo pertenece al recorrido de la función. Además, la función también existe cuando $f(x)=5$ . Pero en cualquier otro valor de $f(x)$ la función no existe, así que el recorrido o imagen de esta función es:

$\text{Im } f= (-\infty,4]\cup \{5\}$

calculo del recorrido de una funcion con una grafica

En algunos tipos de funciones debes hacer un procedimiento especial para calcular el dominio y el recorrido de la función. Este procedimiento depende del tipo de función, por lo que te recomendamos que busques la explicación entera del dominio y el recorrido de las funciones en nuestra página web.

Continuidad de una función

La continuidad de una función se puede estudiar gráficamente. Una función continua es aquella función que se puede representar en una gráfica sin levantar el lápiz del papel.

Función continua

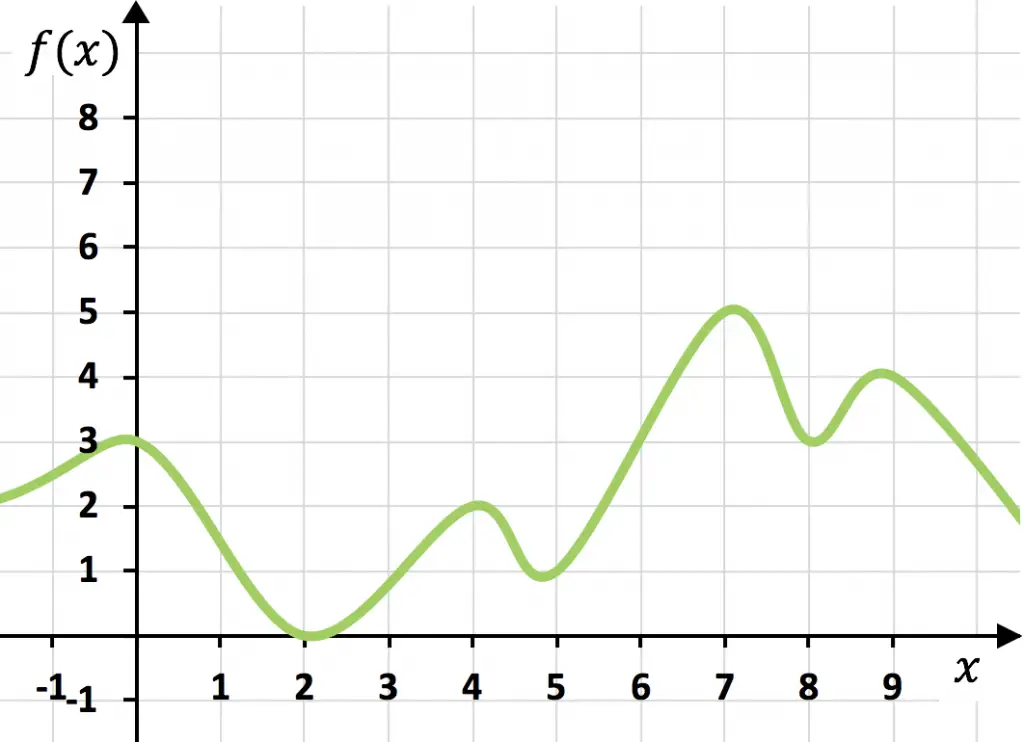
La función anterior es continua porque se puede dibujar en un solo trazo sin levantar la mano del papel.

Por otro lado, cuando en una función no se cumple la condición de continuidad anterior, se dice que es una función discontinua.

Función discontinua

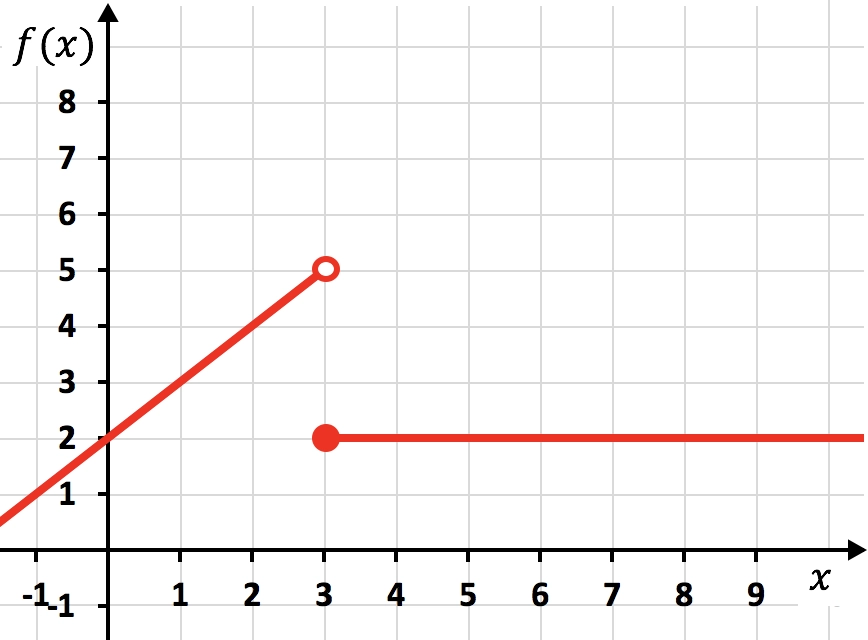
La función anterior es discontinua porque para representarla se deben hacer dos trazos con el lápiz. En este caso, la función deja de ser continua en x=3, por tanto, decimos que x=3 es un punto de discontinuidad.

Tipos de funciones

Las funciones se pueden clasificar en los siguientes tipos:

Funciones polinómicas: funciones cuya expresión algebraica es un polinomio.
Funciones racionales: funciones expresadas en forma de fracción.
Funciones radicales: funciones con raíces.
Funciones exponenciales: funciones en las que la incógnita x forma parte del exponente de una potencia.
Funciones logarítmicas: funciones con logaritmos en su expresión matemática.
Funciones trigonométricas: funciones que están definidas por razones trigonométricas (el seno, el coseno, la tangente,…).
Funciones definidas a trozos: funciones que cambian de expresión algebraica según el tramo al que pertenezca la variable independiente x.
Funciones con valor absoluto: funciones cuya expresión está dentro del signo del valor absoluto.
Funciones simétricas: funciones en las que se puede encontrar como mínimo un eje de simetría en su representación gráfica.
Funciones periódicas: funciones cuya gráfica se va repitiendo cada cierto intervalo (el periodo de la función).

Evidentemente, cada tipo de función tiene sus propias características y peculiaridades, en esta clasificación tan solo hemos puesto su descripción. Pero si estás mas interesad@, puedes buscar la explicación detallada que tenemos en nuestra página web de cada tipo de función.

Composición de funciones

La composición de funciones consiste en evaluar un mismo valor de la variable independiente x en dos funciones o más de manera sucesiva. Por ejemplo, la composición de funciones (g o f)(x) da como resultado la función compuesta g[f(x)].

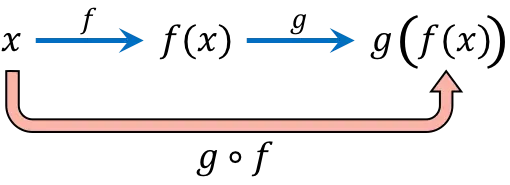
La expresión de la función compuesta $g\circ f$ se lee «f compuesta con g» o «f seguida de g».

Ten en cuenta que el orden es importante en la composición de funciones, primero se aplica la función que está a la derecha del símbolo de composición $(f)$ y luego la función que está a la izquierda del símbolo de composición $(g).$

Vista la definición de función compuesta, vamos a resolver un ejemplo paso a paso de cómo calcular la composición de dos funciones.

Dadas las siguientes dos funciones diferentes:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Calcula la función compuesta $\left(g \circ f\right)(x)$ y evalúala en $x=3.$

La composición de funciones $\left(g \circ f\right)(x)$ significa que debemos hacer la siguiente función compuesta:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Para resolverla, sustituimos $f(x)$ por su expresión algebraica:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

Y ahora cogemos la función de $g(x)=\cfrac{x+4}{2}$ y ponemos la expresión $3x+1$ donde haya una $x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

De esta manera ya hemos calculado la función f compuesta con g:

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Finalmente, para evaluar la función compuesta en $x=3$ simplemente debemos calcular la imagen de la función en dicho valor:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Función inversa

La función inversa, también llamada función recíproca, es aquella función cuyo dominio es el recorrido de otra función (la función original) y cuyo recorrido es el dominio de la función original. La función inversa de la función f se expresa con el símbolo f^-1.

Por lo tanto, la función inversa de f(x) es la función que cumple la siguiente condición:

$\begin{array}{c}f(\color{blue}a\color{black})=\color{red}b\\[1.5ex] \color{teal}\bm{\downarrow} \\[1.5ex] f^{-1}(\color{red}b\color{black})=\color{blue}a \end{array}$

Donde $f^{-1}$ es la función inversa de $f.$

El concepto de función inversa también se puede definir utilizando la composición de funciones, ya que cualquier función compuesta con su función inversa es igual a la función identidad:

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

De manera que si se cumple la ecuación anterior significa que $f^{-1}$ es la función inversa (o función recíproca) de $f.$

Vamos a resolver un ejercicio por pasos de la función inversa para acabar de comprender el concepto.

Determina si las siguientes funciones son inversas entre sí:

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Si las dos funciones son inversas entre sí, se cumplirán las siguientes 2 condiciones:

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Por lo tanto, vamos a comprobar si se cumplen ambas ecuaciones. Primero comprobamos $(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

De modo que $(f \circ g)(x) = x$ sí se cumple.

Ahora vamos a comprobar la igualdad $(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

Y la condición de invertibilidad $(g \circ f)(x) = x$ también se cumple.

En conclusión, como se verifican las dos ecuaciones, las dos funciones son inversas entre sí.

A continuación, puedes ver las dos funciones representadas gráficamente. Fíjate que las gráficas de dos funciones inversas son simétricas respecto a la bisectriz del primer y del tercer cuadrante:

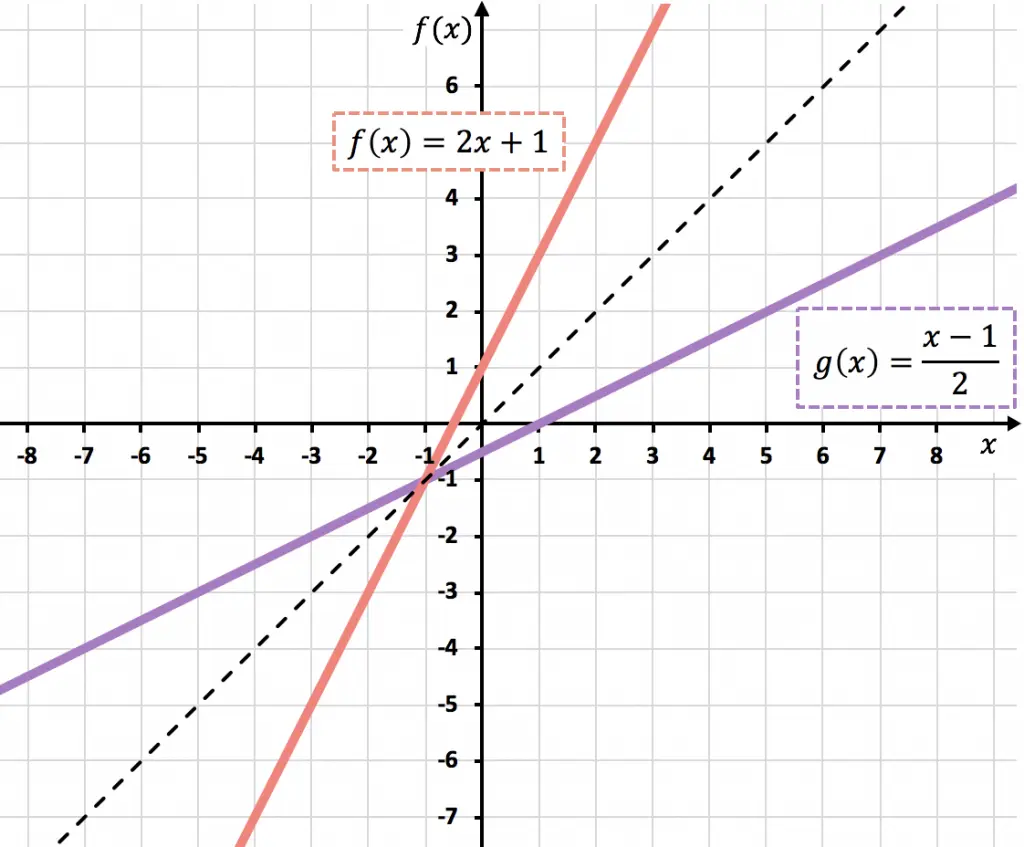
Historia de las funciones

El origen de las funciones es bastante peculiar, ya que no es como una regla científica o una fórmula que se descubre en un año determinado, sino que han tenido que pasar muchísimos años para asimilar este concepto.

Cabe destacar que en las civilizaciones antiguas de Mesopotamia, Egipto y Grecia ya se utilizaban algunas nociones de las funciones. Sin embargo, este no se considera como el inicio de las funciones porque muy probablemente aún no entendían el concepto abstracto de función, es decir, no deberían ser del todo conscientes que utilizaban funciones para hacer cálculos.

Aunque no por unanimidad, la mayor parte de historiadores de las matemáticas atribuyen el inicio de las funciones al científico Nicole Oresme (1323-1382), cuando dijo que las leyes de la naturaleza son como relaciones de dependencia entre dos magnitudes.

Más adelante, el astrónomo Galileo Galilei (1564-1642) realizó estudios sobre el movimiento con los que es evidente que ya se entendía el significado de una función matemática. Entre otros ejemplos, demostró que cada número natural tiene un único cuadrado perfecto y que, por lo tanto, existe una relación matemática entre los números naturales y los cuadrados perfectos.

El término función no aparece hasta finales del siglo XVII, cuando René Descartes (1596-1650), Isaac Newton (1643-1727) y Gottfried Leibniz (1646-1716) definieron una función como una dependencia entre dos cantidades variables. Pero la notación f(x) fue introducida un poco más tarde por Alexis Claude Clairaut (1713-1765) y Leonhard Euler (1707-1783).

A pesar de que en ese momento ya se utilizaban las funciones para hacer cálculos algebraicos, e incluso se publicaban teorías y libros sobre las funciones, su definición aún no estaba completa y pasaron siglos hasta que el matemático Édouard Goursat (1858-1936) en el año 1923 llegó a la definición de función que en la mayoría de libros actuales se usa: «se dice que y es una función de x si a cada valor de x le corresponde un único valor de y. Esta correspondencia se indica mediante la ecuación y=f(x)».