▷ Derivada de un polinomio

En este post te explicamos cómo se calcula la derivada de un polinomio. De modo que encontrarás la fórmula de la derivada de una función polinómica y, además, varios ejemplos resueltos de derivadas de polinomios.

Índice

Fórmula de la derivada de un polinomio

Para calcular la derivada de un polinomio, o de una función polinómica, debemos aplicar la fórmula de la derivada de una potencia a cada término del polinomio y eliminar el término independiente del polinomio.

Por lo tanto, la fórmula de la derivada de un polinomio es la siguiente:

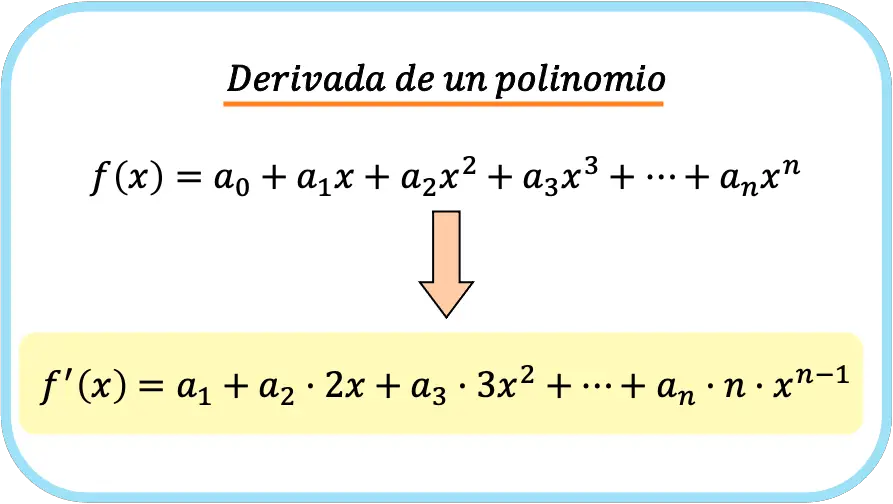
A continuación vamos a demostrar la fórmula de la derivada de una función polinómica:

$\cfrac{d\left(a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n\right)}{dx}$

En primer lugar, utilizamos la fórmula de la derivada de una suma y la fórmula de la derivada de una resta para separar los términos del polinomio:

$\cfrac{d(a_0)}{dx}+\cfrac{d(a_1x)}{dx}+\cfrac{d(a_2x^2)}{dx}+\cfrac{d(a_3x^3)}{dx}+\dots+\cfrac{d(a_nx^n)}{dx}$

La derivada de una constante es igual a cero, por lo que podemos eliminar el término independiente del polinomio:

$\cancelto{0}{\cfrac{d(a_0)}{dx}}+\cfrac{d(a_1x)}{dx}+\cfrac{d(a_2x^2)}{dx}+\cfrac{d(a_3x^3)}{dx}+\dots+\cfrac{d(a_nx^n)}{dx}$

Finalmente, aplicamos la fórmula de la derivada de una potencia para resolver cada una de las derivadas:

$a_1+a_2\cdot 2x+a_3\cdot 3x^2+\dots+a_n\cdot n\cdot x^{n-1}$

➤ Ver: Funciones polinómicas

Ejemplo de la derivada de un polinomio

Para que puedas ver cómo se resuelve la derivada de un polinomio, a continuación te dejamos un ejemplo de este tipo de derivada resuelto paso a paso.

$f(x)=5x^4+3x^2-8x+2$

Para hallar el resultado de la derivada de la función polinómica, tenemos que aplicar la fórmula de la derivada de una potencia a cada término del polinomio:

$f'(x)=5\cdot 4x^{4-1}+3\cdot 2x^{2-1}-8\cdot 1+0$