▷ Derivada de una raíz (fórmula y ejercicios resueltos)

Aquí te explicamos cómo hacer la derivada de una raíz (o función radical). Encontrarás la fórmula para dividir raíces y ejercicios resueltos paso a paso de derivadas de raíces.

Índice

Fórmula de la derivada de una raíz

La derivada de una raíz, o función irracional, es igual a la derivada del radicando (expresión bajo el radical) dividida entre el producto del índice de la raíz por la misma raíz restándole 1 al exponente del radicando.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Sin embargo, si el radicando de la raíz es solamente una x, la fórmula se simplifica. De manera que la derivada de raíz de x es la siguiente:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

En resumen, hay dos fórmulas para derivar una raíz: la primera que se puede usar siempre y la segunda que solo se puede utilizar cuando el radicando es una x.

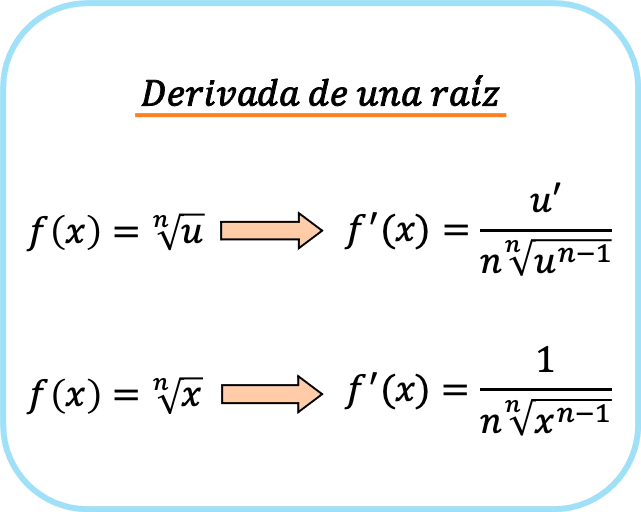
Si te fijas, el término del numerador de la fracción es el que resulta de aplicar la regla de la cadena al hacer la derivada de la raíz. Por eso cuando el radicando es x, en el denominador aparece 1 ya que es la derivada de x.

Ejemplos de derivadas de raíces

Vista la fórmula de la derivada de una función radical, a continuación explicamos varios ejemplos de este tipo de derivadas para que entiendas cómo sacar la derivada de una raíz.

Ejemplo 1: Derivada de una raíz cuadrada

Seguidamente veremos cuál es la derivada de una raíz cuadrada:

$f(x)=\sqrt{x}$

En este caso la expresión dentro de la raíz es tan solo una x, por lo que podemos usar la siguiente fórmula:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Entonces, la derivada de una raíz cuadrada es igual a 1 partido por el producto de 2 por la raíz cuadrada de x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Ejemplo 2: Derivada de una raíz cúbica

$f(x)=\sqrt[3]{x}$

En este ejemplo la expresión bajo la raíz es una x, así que podemos aplicar la siguiente fórmula:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

De manera que la derivada de una raíz cúbica es igual a 1 entre 3 por la raíz cúbica de x al cuadrado:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Ejemplo 3: Derivada de una raíz cuarta

$f(x)=\sqrt[4]{7x-2}$

Ahora no tenemos una x bajo el signo radical, sino que tenemos una expresión algebraica más compleja. Por lo tanto, debemos emplear la fórmula general de la derivada de una raíz:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

La expresión bajo el radical es una función de primer grado, por lo que su derivada es 7. Entonces, la derivada de toda la función es:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Ejemplo 4: Derivada de una raíz dentro de otra

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Para resolver la derivada de esta raíz compuesta por otra raíz, debemos aplicar la siguiente fórmula:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

En este caso debemos utilizar la misma fórmula dos veces de manera sucesiva para calcular la derivada:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Ejercicios resueltos de la derivada de una raíz

Calcula las derivadas de las siguientes raíces:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

Ver solución

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Fórmula de la derivada de una raíz

Ejemplos de derivadas de raíces

Ejemplo 1: Derivada de una raíz cuadrada

Ejemplo 2: Derivada de una raíz cúbica

Ejemplo 3: Derivada de una raíz cuarta

Ejemplo 4: Derivada de una raíz dentro de otra

Ejercicios resueltos de la derivada de una raíz

Deja un comentario Cancelar respuesta