▷ Derivadas (fórmulas, reglas y ejercicios resueltos)

Aquí te explicamos cómo derivar todos los tipos de funciones. Encontrarás las fórmulas de todas las derivadas junto con ejemplos y ejercicios resueltos paso a paso de todos los tipos de derivadas.

Índice

¿Qué son las derivadas?

Las derivadas son reglas matemáticas que sirven para estudiar las funciones. En particular, la derivada de una función en un punto es el resultado de un límite e indica el comportamiento de la función en ese punto.

La derivada de una función se expresa con el signo prima ‘, es decir, la función f'(x) es la derivada de la función f(x).

Geométricamente, el significado de la derivada de una función en un punto es la pendiente de la recta tangente a la función en ese punto.

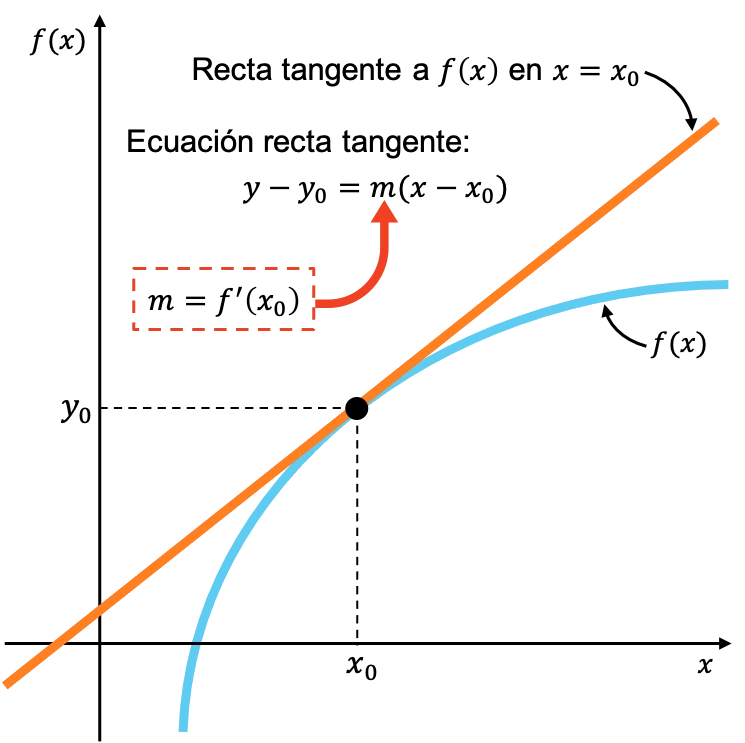
La definición matemática de la derivada de una función es la siguiente:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sin embargo, la derivada de una función no se suele calcular utilizando la fórmula anterior, sino que se aplican reglas de derivación según el tipo de función que sea. En el siguiente apartado se explican todas las fórmulas de derivación.

Ten en cuenta que la derivación es la operación opuesta a la integración, de manera que si derivamos el resultado de una integral obtenemos la función original de nuevo. Puedes ver cómo se integra una función aquí:

➤ Ver: Integrales

Fórmulas de las derivadas

Vista la definición de las derivadas, vamos a ver cómo se hacen explicando cada tipo de derivada con un ejemplo. El objetivo de este post es que entiendas bien el concepto de las derivadas, por lo que si al final tienes dudas de cómo se deriva una función puedes preguntarnos en los comentarios.

Derivada de una constante

La derivada de una constante siempre es igual a cero, independientemente del valor de la constante.

Por lo tanto, para hallar la derivada de una función constante no es necesario hacer ningún cálculo, simplemente la derivada es nula.

Fíjate en los siguientes ejemplos resueltos de derivadas de constantes:

$\begin{array}{c}f(x)=3 \qquad \longrightarrow\qquad f'(x)=0\\[3ex]g(x)=-5 \qquad \longrightarrow\qquad g'(x)=0\\[3ex]h(x)=291 \qquad \longrightarrow\qquad h'(x)=0\end{array}$

Derivada de una función lineal

La derivada de una función lineal es el coeficiente del término de primer grado, es decir, la derivada de una función lineal f(x)=Ax+B es igual a A

Fíjate en los siguientes ejemplos cómo se han derivado este tipo de funciones:

$\begin{array}{c}f(x)=3x-1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Derivada de una potencia

La derivada de una potencia, o función potencial, es el producto del exponente de la potencia por la base elevada al exponente menos 1.

Por lo tanto, para derivar una potencia solamente tenemos que multiplicar la función por el exponente y restarle una unidad al exponente.

Por ejemplo, la derivada de la potencia x elevada al cubo es:

$f(x)=x^3 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=3\cdot x^{3-1}=3x^2$

Puedes practicar de hacer ejercicios (y más difíciles) de este tipo de derivadas aquí:

➤ Ver: ejercicios resueltos de la derivada de una potencia

Derivada de una raíz

La derivada de una raíz, o función irracional, es igual a uno partido por el producto del índice de la raíz por la misma raíz restándole 1 al exponente del radicando.

A modo de ejemplo, seguidamente puedes ver resuelta la derivada de la raíz cuadrada de x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

➤ Ver: ejercicios resueltos de la derivada de una raíz

Derivada de una función exponencial

La derivada de una función exponencial depende de si la base es el número e o cualquier otro número. De manera que hay dos fórmulas para derivar este tipo de funciones y deberemos utilizar la que corresponda según la base de la potencia:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1pt, boxsep=1.8mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{l}f(x)=a^x \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=a^x\cdot \ln(a)\\[3ex] f(x)=e^x \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=e^x \end{array} \end{empheq}$

A continuación puedes ver dos derivadas resueltas de este tipo de funciones:

$f(x)=7^{x} \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=7^x\cdot \ln(7)$

$f(x)=e^{x} \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=e^x$

➤ Ver: ejercicios resueltos de la derivada de una función exponencial

Derivada de una función logarítmica

La derivada de una función logarítmica depende de la base del logaritmo, ya que si el logaritmo es natural se debe aplicar una fórmula para hallar la derivada y si el logaritmo tiene como base otro número se debe usar otra regla.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1pt, boxsep=1.8mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{l}f(x)=\ln(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x}\\[3ex] f(x)=\log_a(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x\cdot\ln(a)}\end{array} \end{empheq}$

Por ejemplo, la derivada del logaritmo en base tres de x es:

$f(x)=\log_3(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x\cdot\ln(3)}$

➤ Ver: ejercicios resueltos de la derivada de una función logarítmica

Derivadas trigonométricas

Las tres derivadas trigonométricas principales son la derivada de la función seno, de la función coseno y de la función tangente, cuyas fórmulas son las siguientes:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1pt, boxsep=1.8mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{l}f(x)=\text{sen}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x)\\[2.5ex] f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)\\[1.1ex]f(x)=\text{tan}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\text{cos}^2(x)}\end{array} \end{empheq}$

Lógicamente, existen más tipos de funciones trigonométricas, como por ejemplo la función secante, la cosecante, la cotangente, las funciones trigonométricas hiperbólicas, las funciones trigonométricas inversas, etc. Pero las reglas más utilizadas para derivar son estas tres de arriba.

Reglas de derivación

Cuando tenemos operaciones con funciones las derivadas se resuelven de manera diferente. Para ello, debemos emplear la reglas de derivación, que nos permiten derivar sumas, restas, multiplicaciones y divisiones de funciones.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{l}z(x)=f(x)\pm g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)\pm g'(x)\\[4ex] z(x)=f(x)\cdot g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\\[4ex]z(x)=\cfrac{f(x)}{g(x)} \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array} \end{empheq}$

Por lo tanto, para resolver derivadas con operaciones no solo tenemos que aplicar las reglas de derivación, sino que también debemos utilizar la fórmula de cada tipo de derivada.

Para que veas cómo hallar este tipo de derivadas, vamos a resolver varios ejercicios a continuación:

Derivada de una suma:

$f(x)=3x^2+5x$

$f'(x)=6x+5$

Como puedes ver, para resolver la derivada de toda la función se ha aplicado la fórmula de la derivada de una potencia a cada término de la suma.

Derivada de un producto:

$f(x)=4^{x}\cdot \text{sen}(x)$

La derivada del primer término del producto es 4^x·ln(4), y la derivada del seno es el coseno. Por lo tanto, la derivada de la multiplicación es:

$f'(x)=4^{x}\cdot \ln (4) \cdot \text{sen}(x) +4^{x}\cdot \text{cos}(x)$

Derivada de un cociente:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Tanto en el numerador como en el denominador de la fracción tenemos un polinomio, así que para sacar la derivada debemos utilizar la fórmula de la derivada de un cociente, la fórmula de la derivada de una suma (o resta) y la fórmula de la derivada de una potencia:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Regla de la cadena

La regla de la cadena es una fórmula que sirve para derivar funciones compuestas. La regla de la cadena establece que la derivada de una función compuesta f(g(x)) es igual a la derivada f'(g(x)) multiplicada por la derivada g'(x).

Este concepto de las derivadas normalmente es más difícil de asimilar, por lo que resolveremos un ejercicio paso a paso a modo de ejemplo:

$f(x)=\text{sen}(x^3)$

Efectivamente, se trata de una composición de funciones porque tenemos la función x³ dentro de la función seno, por lo tanto, tenemos que usar la regla de la cadena para hallar la derivada de la función compuesta.

Por una parte, la derivada del seno es el coseno, por lo que la derivada de la función de afuera será el coseno con el mismo argumento del seno:

$f\bigl(g(x)\bigr)=\text{sen}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3)$

Y, por otra parte, calculamos la derivada de x³ usando la fórmula de la derivada de una potencia:

$g(x)=x^3\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2$

De manera que la derivada de toda la función compuesta es el producto de ambas derivadas:

$f(x)=\text{sen}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3)\cdot 3x^2$

➤ Ver: ejercicios resueltos de derivadas con la regla de la cadena

Derivabilidad de una función

La continuidad y la derivabilidad de una función en un punto se relacionan de la siguiente manera:

Si una función es derivable en un punto, la función es continua en ese punto.
Si una función no es continua en un punto, tampoco es derivable en ese punto.

Sin embargo, el recíproco de este teorema es falso, es decir, que una función sea continua en un punto no significa que siempre sea derivable en ese punto.

También se puede ver si una función es derivable o no en un punto a partir de su representación gráfica:

Si es un punto suave la función es derivable en ese punto.
Si es un punto anguloso la función es continua pero no derivable en ese punto.

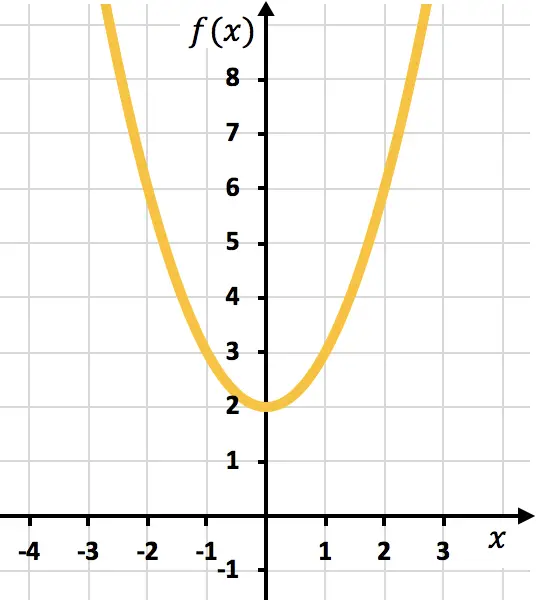
Punto suave en x=0:
función continua y derivable en ese punto.

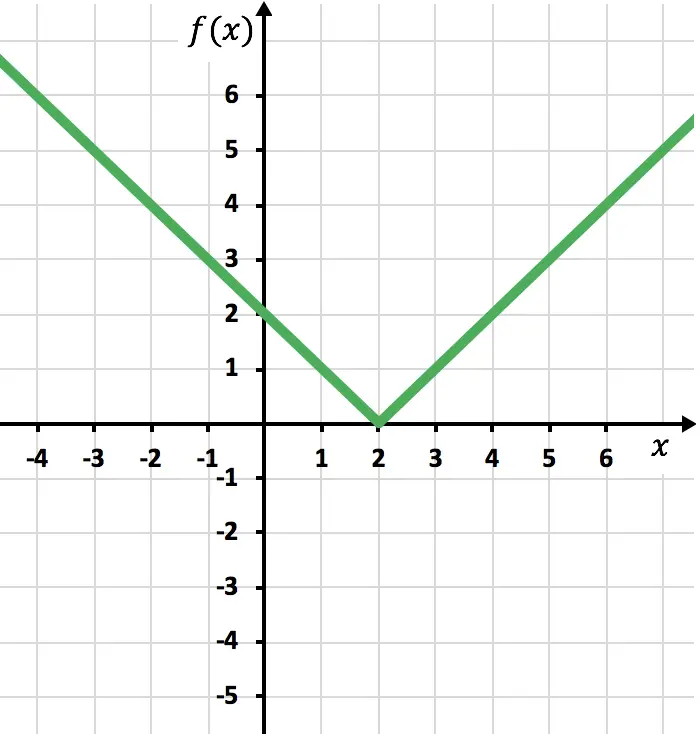
Punto anguloso en x=2:
función continua pero no derivable en ese punto.

También se puede saber si una función definida a trozos es derivable en un punto calculando las derivadas laterales en ese punto:

Si las derivadas laterales en un punto no son iguales, la función no es derivable en ese punto:

$f'(x_o^-) \neq f'(x_o^+) \ \longrightarrow$ No es derivable en $x_o$

Si las derivadas laterales en un punto coinciden, la función es derivable en ese punto:

$f'(x_o^-) = f'(x_o^+) \ \longrightarrow$ Sí es derivable en $x_o$

Veamos ahora un ejemplo de cómo calcular la derivada de una función definida a trozos en un punto:

Estudia la continuidad y la derivabilidad de la siguiente función definida a trozos en el punto x=2:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.$

Las funciones de los dos tramos son continuas en sus respectivos intervalos, sin embargo, debemos mirar si la función es continua en el punto crítico x=2. Para ello, resolvemos los límites laterales de la función en el punto:

$\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(3x^2-6x\bigr) = 3\cdot2^2-6\cdot2=12-12=\bm{0}$

$\lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} 6\ln (x-1) = 6\ln (2-1)=6 \ln 1=6 \cdot 0= \bm{0}$

Los límites laterales en el punto crítico nos han dado el mismo resultado, por tanto, la función es continua en el punto x=2.

Una vez sabemos que la función es continua en x=2, vamos a estudiar la derivabilidad de la función en ese punto. Para ello, calculamos las derivadas laterales de la función definida a trozos:

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.$

Ahora evaluamos cada derivada lateral en el punto crítico:

$f'(2^-)=6\cdot2-6=12-6 = \bm{6}$

$f'(2^+)=\cfrac{6}{2-1} = \cfrac{6}{1} = \bm{6}$

Las dos derivadas laterales nos han dado el mismo resultado, por tanto, la función es derivable en x=2 y el valor de la derivada es 6:

$f'(2^-) = f'(2^+) = 6 \ \longrightarrow \ \bm{f'(2) = 6}$

Por otro lado, si las derivadas laterales nos hubiesen dado un resultado diferente, significaría que la función no es derivable en x=2. Es decir, que la derivada en este punto no existiría.

➤ Ver: ejercicios resueltos de la derivabilidad de una función