▷ Integrales de funciones exponenciales

En este post te explicamos cómo se resuelven las integrales de funciones exponenciales. Por lo tanto, encontrarás las fórmulas de las integrales de funciones exponenciales y, además, podrás ver varios ejemplos resueltos de este tipo de integrales.

Índice

Fórmula de la integral de una función exponencial

La integral de una función exponencial, es decir, de una constante elevada a la x, es igual a la función exponencial partido por el logaritmo neperiano de su base.

$\displaystyle \int a^x dx=\cfrac{a^x}{\ln a}+C$

Cuando la base de la función exponencial es el número e, se da el caso de que el logaritmo neperiano de e da como resultado 1. Por lo tanto, la integral de una función exponencial con base e es igual a la misma función exponencial con base e. Así pues, la integral de e^x es la propia función e^x.

$\displaystyle \int e^x dx=e^x+C$

Ten en cuenta que si el exponente es una función, entonces la derivada de dicha función debe estar multiplicando a la función exponencial en la integral:

$\displaystyle \int a^u\cdot u'\cdot dx=\cfrac{a^u}{\ln a}+C$

$\displaystyle \int e^u \cdot u'\cdot dx=e^u+C$

En definitiva, las fórmulas para resolver integrales de funciones exponenciales son las siguientes:

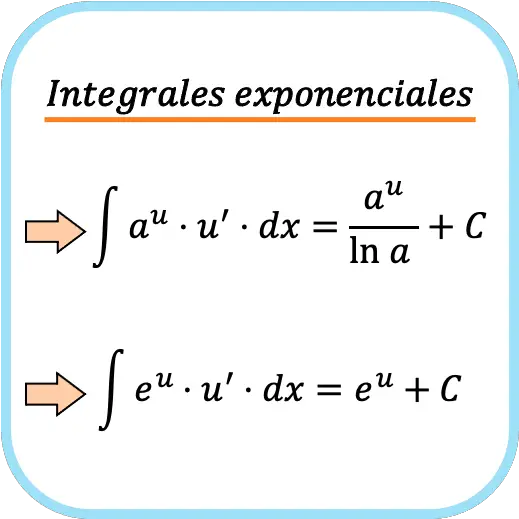
fórmula de la integral de una función exponencial

Fíjate que la fórmula de las integrales exponenciales se puede deducir de la fórmula de la derivada de una función exponencial.

➤ Ver: Derivada de una función exponencial

Ejemplos de integrales de funciones exponenciales

Después de ver cuál es la fórmula que nos permite calcular integrales de funciones exponenciales, vamos a ver dos ejemplos resueltos para acabar de entender cómo se resuelven estos tipos de integrales.

Ejemplo 1: integral de una función exponencial de base constante

$\displaystyle\int 5^{2x} dx$

La integral que queremos resolver es de una función exponencial cuya base es diferente del número de Euler, por lo que tenemos que usar la siguiente fórmula para determinar su resultado:

$\displaystyle \int a^u\cdot u'\cdot dx=\cfrac{a^u}{\ln a}+C$

No obstante, para poder aplicar la fórmula necesitamos que la derivada del exponente esté multiplicando a la función. La derivada de 2x es 2, por lo que multiplicamos y dividimos por dos y luego sacamos el denominador fuera de la integral:

$\displaystyle\int 5^{2x} dx=\int 5^{2x}\cdot \cfrac{2}{2} \cdot dx =\cfrac{1}{2}\int 5^{2x}\cdot 2 \cdot dx$

Finalmente, una vez hemos logrado que la función esté multiplicada por la derivada del exponente, podemos utilizar la fórmula que hemos visto más arriba para solucionar la integral exponencial:

$\displaystyle\cfrac{1}{2}\int 5^{2x}\cdot 2 \cdot dx=\cfrac{1}{2}\cdot \cfrac{5^{2x}}{\ln 5}+C=\cfrac{5^{2x}}{2\ln 5}+C$

Ejemplo 2: integral de una función exponencial de base e

$\displaystyle\int e^{7x+1} dx$

En este caso la base de la función exponencial es el número e, así que debemos usar la fórmula para calcular integrales de funciones exponenciales con base e:

$\displaystyle \int e^u \cdot u'\cdot dx=e^u+C$

Sin embargo, necesitamos que la función exponencial esté multiplicada por la derivada del exponente para poder resolver la integral. Dicha derivada es una constante (7), así que multiplicamos y dividimos la función por su derivada y luego sacamos el denominador fuera de la integral:

$\displaystyle\int e^{7x+1} dx=\int e^{7x+1}\cdot \cfrac{7}{7} \cdot dx =\cfrac{1}{7}\int e^{7x+1}\cdot 7 \cdot dx$

Por último, aplicamos la fórmula para resolver la integral exponencial:

$\displaystyle\cfrac{1}{7}\int e^{7x+1}\cdot 7 \cdot dx=\cfrac{ e^{7x+1}}{7}+C$

➤ Ver: Integrales logarítmicas

Ejercicios resueltos de integrales exponenciales

Resuelve las siguientes integrales exponenciales:

$\text{A) } \displaystyle\int 6^x \ dx$

$\text{B) } \displaystyle\int 3^x\cdot 4^x \ dx$

$\text{C) } \displaystyle\int e^{10x-2} \ dx$

$\text{D) } \displaystyle\int x\cdot e^{x^2-8} \ dx$

$\text{E) } \displaystyle\int \frac{3^{\ln x}}{x}\ dx$

Ver solución

$\text{A) } \displaystyle\int 6^x \ dx=\cfrac{6^x}{\ln 6}+C$

$\text{B) } \displaystyle\int 3^x\cdot 4^x \ dx=\int (3\cdot 4)^x\ dx=\int 12^x \ dx=\cfrac{12^x}{\ln 12}+C$

$\text{C) } \displaystyle\int e^{10x-2} \ dx=\int \cfrac{10}{10}\cdot e^{10x-2} \ dx=\cfrac{1}{10}\int 10 \cdot e^{10x-2} \ dx= \cfrac{e^{10x-2}}{10}+ C$

$\text{D) } \displaystyle\int x\cdot e^{x^2-8} \ dx=\int\cfrac{2}{2}\cdot x\cdot e^{x^2-8} \ dx=\cfrac{1}{2}\int 2x\cdot e^{x^2-8} \ dx =\cfrac{e^{x^2-8}}{2}+ C$

$\text{E) } \displaystyle\int \frac{3^{\ln x}}{x}\ dx= \int \frac{1}{x}\cdot 3^{\ln x}\ dx= \cfrac{3^{\ln x}}{\ln 3} + C$

Fórmula de la integral de una función exponencial

Ejemplos de integrales de funciones exponenciales

Ejemplo 1: integral de una función exponencial de base constante

Ejemplo 2: integral de una función exponencial de base e

Ejercicios resueltos de integrales exponenciales

Deja un comentario Cancelar respuesta