En este post explicamos qué son las funciones simétricas (funciones pares e impares) y cómo estudiar la simetría de una función. También podrás ver las propiedades que tienen este tipos de funciones y, finalmente, podrás practicar con ejercicios resueltos paso a paso de funciones simétricas.
Índice
¿Qué es una función simétrica?
Una función simétrica es una función en la que se puede encontrar un eje de simetría en su representación gráfica. Existen dos tipos de funciones simétricas: las funciones pares, que son simétricas respecto al eje Y, y las funciones impares, que son simétricas respecto al origen de coordenadas.
Recuerda que un eje de simetría es una línea imaginaria que divide un elemento cualquiera en dos partes de manera que sus puntos opuestos sean equidistantes entre sí.
Funciones pares
Las funciones pares son funciones que son simétricas respecto al eje de ordenadas, es decir, el eje Y es un eje de simetría de la función.
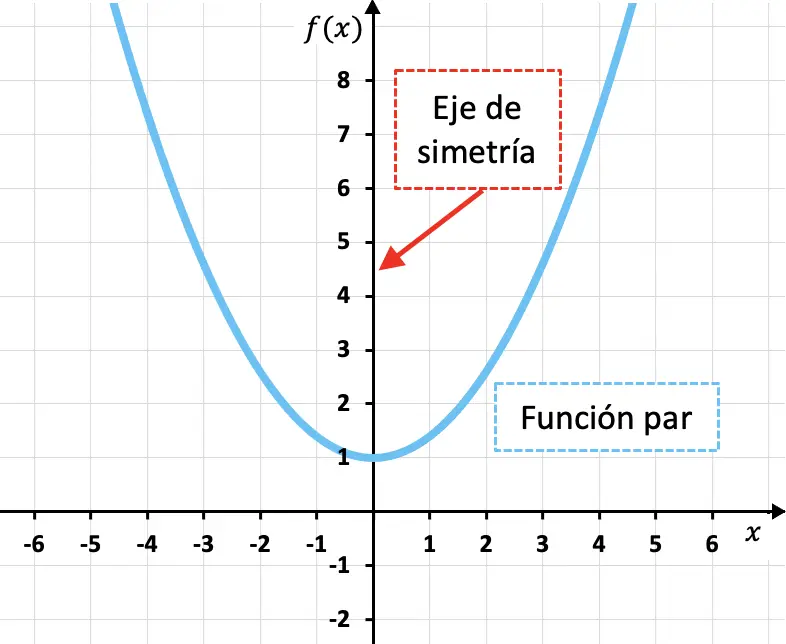
Como puedes ver en la función cuadrática representada arriba, la imagen de una función par para cualquier valor de la variable independiente (x) es equivalente a la imagen de la función para el valor opuesto (-x). Es decir, matemáticamente una función es par si cumple la siguiente condición:
Las funciones pares son un tipo de funciones simétricas, veamos ahora cómo son las funciones impares.
Funciones impares
Las funciones impares son aquellas funciones que son simétricas respecto al origen de coordenadas, es decir, respecto al punto (0,0).
A continuación puedes ver una función impar representada gráficamente:
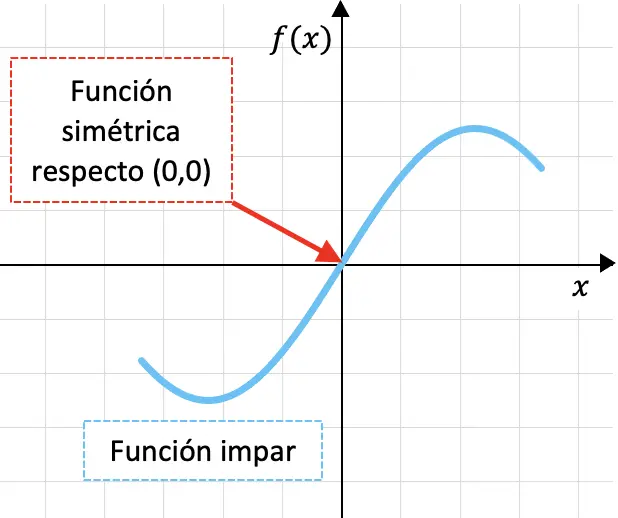
Que una función sea simétrica respecto al origen de coordenadas significa que si plegamos la gráfica de la función primero por el eje OY y luego por el eje OX, la gráfica de la función se solaparía.
Algebraicamente, una función es impar si se cumple la siguiente relación entre sus imágenes:
Saber la simetría de una función es muy útil para representarla, ya que solo sabiendo una mitad de la gráfica podemos graficar la otra parte rápidamente.
Cómo encontrar la simetría de una función
Para estudiar la simetría de una función debemos calcular la imagen de 
, es decir, debemos calcular 
Entonces, según el resultado de la imagen, la simetría de la función será:
- Si se cumple
, la función es par y, por tanto, es simétrica respecto al eje Y. - Si se cumple , la función es impar y, por tanto, es simétrica respecto al origen de coordenadas.
- Si no se cumple ninguna de las anteriores condiciones, se trata de una función asimétrica (no tiene ningún eje de simetría).
Por ejemplo, vamos a analizar la simetría de la siguiente función cúbica:
Para estudiar la simetría de la función, calculamos 
La expresión algebraica obtenida es equivalente a la expresión de la función original pero cambiada de signo, o dicho de otra forma, se cumple la siguiente igualdad:
De manera que la función es impar y, por tanto, es simétrica respecto al origen de coordenadas (0,0).
Propiedades de las funciones simétricas
Las funciones simétricas tienen las siguientes características:
- La suma de dos funciones pares/impares es igual a otra función par/impar.
- El producto de dos funciones pares o dos funciones impares da como resultado una función par.
- La derivada de una función par/impar es una función impar/par.
- La composición entre dos funciones pares/impares es equivalente a una función par/impar.
- La única función que es par e impar a la vez, es decir, que es simétrica respecto al eje OY y respecto al origen, es la función
Ejercicios resueltos de la simetría de una función
Ejercicio 1
Encuentra la simetría de la siguiente función:
Para calcular la simetría de la función, tenemos que evaluar
Cualquier potencia de número negativo elevado a un exponente para da como resultado un número positivo, por lo que en este caso se cumple la siguiente ecuación:
De manera que la función es par y, en consecuencia, es simétrica respecto al eje de las ordenadas (eje Y).
Ejercicio 2
Estudia la simetría de la siguiente función racional:
Para determinar la simetría de la función, hacemos
En este problema no se cumple ninguna condición de simetría, porque la imagen de no es igual ni a 
ni a 
Así que la función no tiene ningún eje de simetría, sino que es una función asimétrica.
Ejercicio 3
Calcula la simetría de la siguiente función:
Para analizar la simetría de la función tenemos que calcular
![\begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-0ccff6541b7e51dea1c295e400dc1fc0_l3.svg "Rendered by QuickLaTeX.com")
En este caso, la expresión obtenida es como la expresión original pero cambiada de signo, por lo que se cumple la siguiente ecuación:
Así que la función es impar y, por tanto, es simétrica respecto al origen de coordenadas (0,0).
Muy buena página y muy bien explicado todo muchas gracias.
¡Gracias José! Me alegro de que te guste.